A quite different lens — and one that gets us a step closer to the way convolutions are used in neural nets — is convolution as a kind of information aggregation, but an aggregation from the perspective of a specific point: the point at which the convolution is being evaluated.
The output point wants to summarize information about the value of f(x) across the function’s full domain, but it wants to do so according to some specific rule.
- Perhaps it only cares about the value of f at points one unit away from it, and doesn’t need to know about points outside that window.
- Perhaps it cares more about points closer to itself in space, but the extent to which it cares decays smoothly, rather than dropping off to zero outside of some fixed window, like in the first example.
- Or, perhaps it cares most about points far away from it.
All of these different kinds of aggregations can fall under the framework of a convolution, and they are expressed through the function g(x).
From a mathematical viewpoint, convolutions can be seen as calculating a weighted sum of the values of f(x), and doing so in a way where the contribution from each x is determined by its distance between it and your output point t.
More precisely, the weight is determined by asking “if there were a copy of g(x) centered at each point x, what would the value of that copied function be, if we evaluated it at the output point t”.
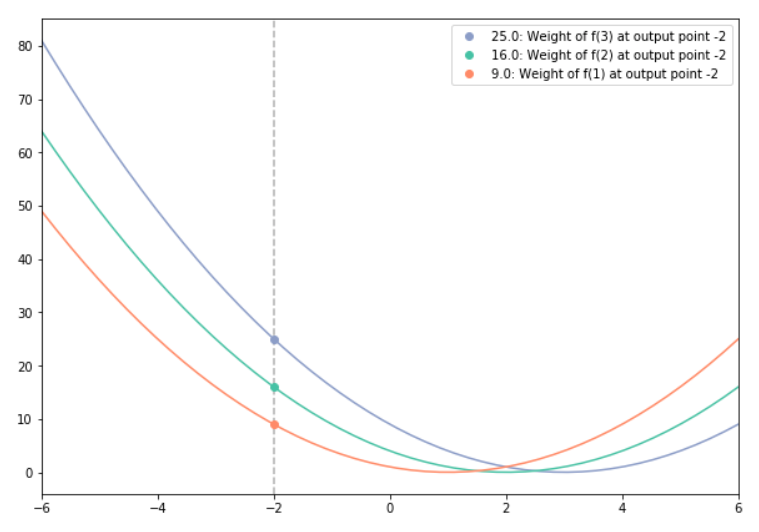
To visualize this, take a look at the plot below. In this example, we are using g(x) = x², and imagining how we’d calculate weights for a weighted sum being calculated at x = -2.
- The orange curve is g(x), but centered at x=1, and its value at x=-2 is 9.
- The green curve is g(x), but centered at x=2, and its value at x=-2 is 16.
- The purple curve is g(x), but centered at x=3, and its value at x=-2 is 25.
If we were to imagine that f is a function that only takes non-zero values at 1, 2, and 3, we could calculate (f * g)(-1) as: 9f(1) + 16f(2) + 25*f(3)
- When we focus attention on a specific input point, each point’s copy of g(x) is answering the question “how will the f(x) information from this point be spread out”.
- When we focus a specific output point, we’re asking “how strong is the contribution from each other point to the aggregation of f(x) at this output point”.
Each vertical line on the multiple-copies graph from the prior section corresponds to the convolution at a given x, and reading off the intersections of that line with each g(x) copy gives you the weight of f(x) at the x where that copy is centered.