In a convolution, rather than smoothing the function created by the empirical distribution of datapoints, we take a more general approach, which allows us to smooth any function f(x).
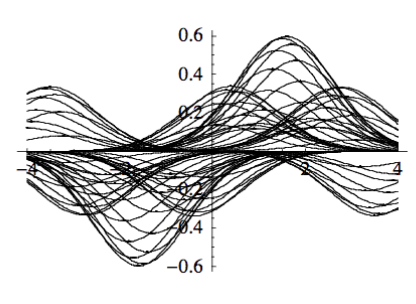
We take some kernel function g(x), and at each point in the integral we place a copy of g(x), scaled up by — which is to say, multiplied by — the value of f(x) at that point.
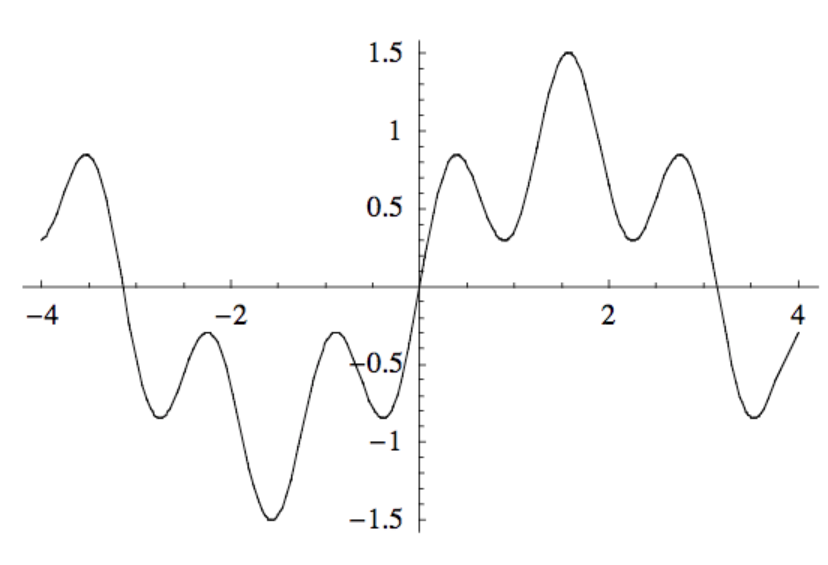
An original f(x), the noisy signal we want to smooth.
The “kernel weighting” process — here a Gaussian function is placed centered at each point, and is being scaled up by the value of f(x) at that point
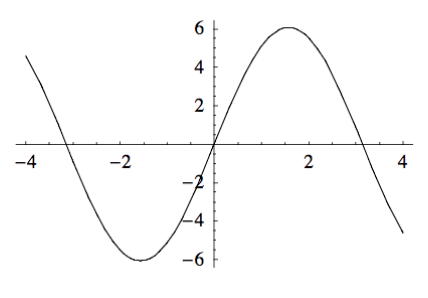
What you get when you sum up all of those scaled kernels: the plot of the convolution of (f*g)(x).