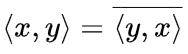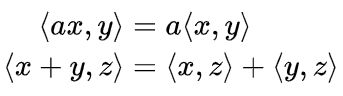In linear algebra, an inner product space is a vector space with an additional structure called an inner product.
This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors.
Inner products allow the rigorous introduction of intuitive geometrical notions such as the length of a vector or the angle between two vectors.
They also provide the means of defining orthogonality between vectors (zero inner product).
Inner product spaces generalize Euclidean spaces (in which the inner product is the dot product, also known as the scalar product) to vector spaces of any (possibly infinite) dimension, and are studied in functional analysis.
Formally, an inner product space is a vector space V over the field F together with an inner product, i.e., with a map
⟨·, ·⟩ : V × V → F
that satisfies the following 3 properties for all vectors x, y, z ∈ V and all scalars a ∈ F:
1. Conjugate symmetry
2. Linearity in the first argument
3. Positive-definite