There are two main ways of measuring the depth of a model.
The first view is based on the number of sequential instructions that must be executed to evaluate the architecture.
We can think of this as the length of the longest path through a flow chart that describes how to compute each of the model’s outputs given its inputs.
Just as two equivalent computer programs will have different lengths depending on which language the program is written in, the same function may be drawn as a flowchart with different depths depending on which functions we allow to be used as individual steps in the flowchart.
The figure below illustrates how this choice of language can give two different measurements for the same architecture.
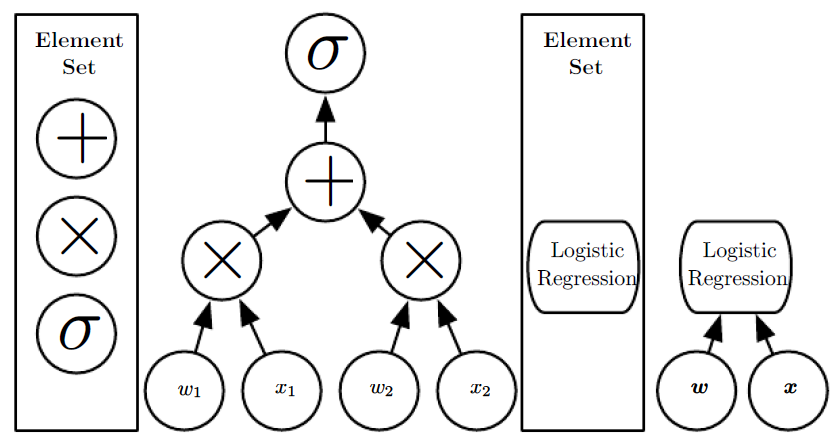
Illustration of computational graphs mapping an input to an output where each node performs an operation.
Depth is the length of the longest path from input to output but depends on the definition of what constitutes a possible computational step.
The computation depicted in these graphs is the output of a logistic regression model, σ(wT x), where σ is the logistic sigmoid function.
- If we use addition, multiplication and logistic sigmoids as the elements of our computer language, then this model has depth three.
- If we view logistic regression as an element itself, then this model has depth one.
Another approach, used by deep probabilistic models, regards the depth of a model as being not the depth of the computational graph but the depth of the graph describing how concepts are related to each other.
In this case, the depth of the flowchart of the computations needed to compute the representation of each concept may be much deeper than the graph of the concepts themselves.
This is because the system’s understanding of the simpler concepts can be refined given information about the more complex concepts.For example, an AI system observing an image of a face with one eye in shadow may initially only see one eye.
After detecting that a face is present, it can then infer that a second eye is probably present as well.
In this case, the graph of concepts only includes two layers—a layer for eyes and a layer for faces — but the graph of computations includes 2n layers if we refine our estimate of each concept given the other n times.
Because it is not always clear which of these two views—the depth of the computational graph, or the depth of the probabilistic modeling graph — is most relevant, and because different people choose different sets of smallest elements from which to construct their graphs, there is no single correct value for the depth of an architecture, just as there is no single correct value for the length of a computer program.
Nor is there a consensus about how much depth a model requires to qualify as “deep.”
However, deep learning can safely be regarded as the study of models that either involve a greater amount of composition of learned functions or learned concepts than traditional machine learning does.