What are Activation functions?
Activation functions are really important for a Artificial Neural Network to learn and make sense of something really complicated and Non-linear complex functional mappings between the inputs and response variable.
They introduce non-linear properties to our Network.
Their main purpose is to convert a input signal of a node in a A-NN to an output signal.
That output signal now is used as a input in the next layer in the stack.Specifically in A-NN we do the sum of products of inputs(X) and their corresponding Weights(W) and apply a Activation function f(x) to it to get the output of that layer and feed it as an input to the next layer.
Why can’t we do it without activating the input signal?
If we do not apply a Activation function then the output signal would simply be a simple linear function.
A linear function is just a polynomial of one degree.
Now, a linear equation is easy to solve but they are limited in their complexity and have less power to learn complex functional mappings from data.A Neural Network without Activation function would simply be a Linear regression Model, which has limited power and does not performs good most of the times.
We want our Neural Network to not just learn and compute a linear function but something more complicated than that.
Also without activation function our Neural network would not be able to learn and model other complicated kinds of data such as images, videos , audio, speech etc.
That is why we use Artificial Neural network techniques such as Deep learning to make sense of something complicated, high dimensional, non-linear big datasets, where the model has lots and lots of hidden layers in between and has a very complicated architecture which helps us to make sense and extract knowledge form such complicated big datasets.
So why do we need Non-Linearities?
Non-linear functions are those which have degree more than one and they have a curvature when we plot a Non-Linear function.
Now we need a Neural Network Model to learn and represent almost anything and any arbitrary complex function which maps inputs to outputs.
Neural-Networks are considered Universal Function Approximators.
It means that they can compute and learn any function at all.
Almost any process we can think of can be represented as a functional computation in Neural Networks.Hence it all comes down to this, we need to apply a Activation function
f(x)so as to make the network more powerfull and add ability to it to learn something complex and complicated form data and represent non-linear complex arbitrary functional mappings between inputs and outputs.Hence using a non linear Activation we are able to generate non-linear mappings from inputs to outputs.
Also another important feature of a Activation function is that it should be differentiable.
We need it to be this way so as to perform backpropogation optimization strategy while propogating backwards in the network to compute gradients of Error(loss) with respect to Weights and then accordingly optimize weights using Gradient descend or any other Optimization technique to reduce Error.
Just always remember to do :
“Input times weights , add Bias and Activate”
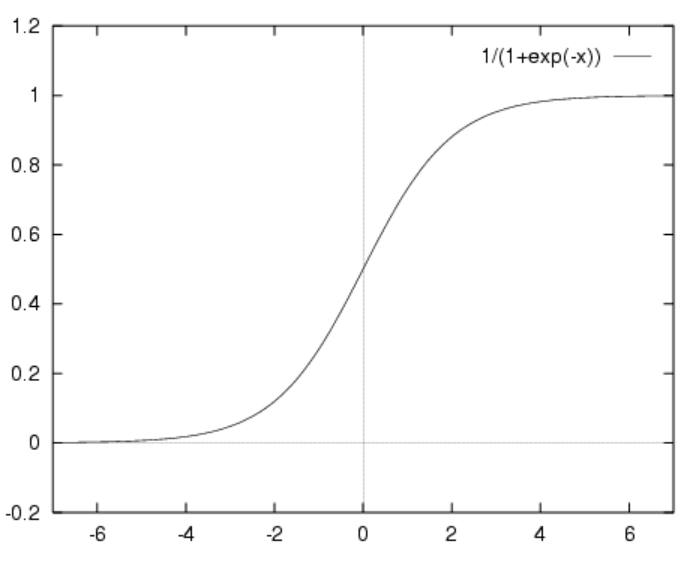
Sigmoid Activation function
It is a activation function of form
f(x) = 1 / 1 + exp(-x).
Its range is between 0 and 1.
It is a S — shaped curve.
It is easy to understand and apply but it has major reasons which have made it fall out of popularity:-
- Vanishing gradient problem
- Its output isn’t zero centered.
It makes the gradient updates go too far in different directions.
0 < output < 1, and it makes optimization harder.- Sigmoids saturate and kill gradients.
- Sigmoids have slow convergence.
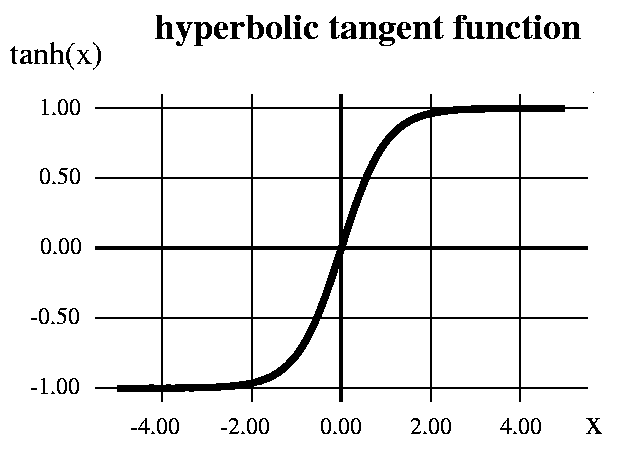
Hyperbolic Tangent function - Tanh
It’s mathamatical formula is
f(x) = 1 — exp(-2x) / 1 + exp(-2x)
Now it’s output is zero-centered because its range in between -1 to 1 i.e -1 < output < 1.Hence optimization is easier in this method hence in practice it is always preferred over Sigmoid function .
But still it suffers from the vanishing gradient problem.
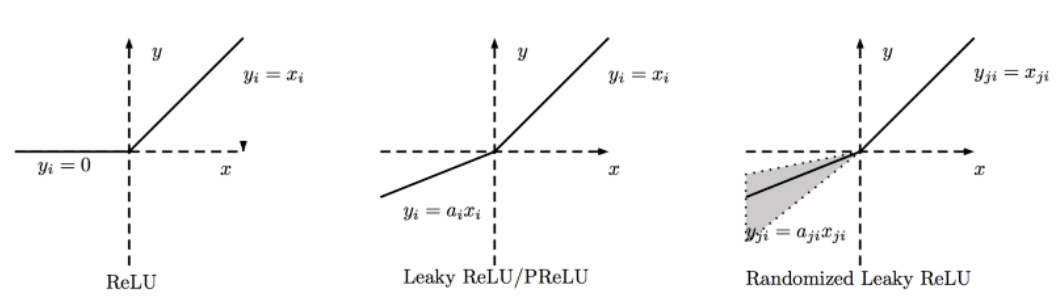
ReLU - Rectified Linear units
It has become very popular in the past couple of years.
It was recently proved that it had 6 times improvement in convergence from Tanh function.
It’s just
R(x) = max(0,x)i.e if x < 0 , R(x) = 0 and if x >= 0 , R(x) = x.Hence as seeing the mathamatical form of this function we can see that it is very simple and efficinent .
A lot of times in Machine learning and computer science we notice that most simple and consistent techniques and methods are only preferred and are best.
Hence it avoids and rectifies vanishing gradient problem .
Almost all deep learning Models use ReLU nowadays.But its limitation is that it should only be used within hidden layers of a neural network model.
Hence for output layers we should use a softmax function for a classification problem to compute the probabilites for the classes, and for a regression problem it should simply use a linear function.
Another problem with ReLU is that some gradients can be fragile during training and can die.
It can cause a weight update which will makes it never activate on any data point again.
Simply saying that ReLU could result in Dead Neurons.To fix this problem another modification was introduced called Leaky ReLU to fix the problem of dying neurons.
It introduces a small slope to keep the updates alive.We then have another variant made form both ReLU and Leaky ReLU called Maxout function.
towardsdatascience.com/activation-functions-and-its-types-which-is-better-a9a5310cc8f