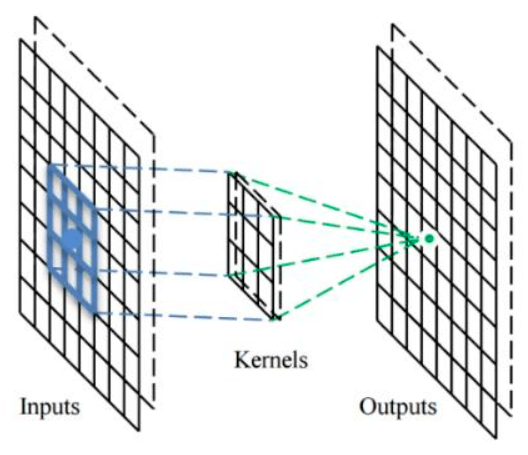
What’s actually difficult and unintuitive about the jump from traditional convolution to network convolution is that, when we see localized aggregation happening in the neural network context, we typically frame it as happening through a weighting kernel centered at the aggregation point, which pulls in information from the surroundings according to that kernel.
A convolution filter in a network is composed the weights of all the input points surrounding the output point (as well as the output point itself).
However, as you may have recall from the discussion earlier in the post, traditional mathematical convolution doesn’t actually center its g(x) weight kernels around the output point.
In the convolution formula, copies of g(x) get centered at each input point, and the value of that copy at a given output determines the weight of that input point there.
So, confusingly, filter kernels as we know them in network convolution are not the same thing as g(x) in the convolution formula.
If we wanted to take a network filter and apply it using the convolution formula, we would have to flip it (in the 1D case) or flip it diagonally (in the 2D case).
And, going in reverse, if we wanted to take a g(x) from the convolution integral and use it as an output-centered filter, that filter would be g(-x).
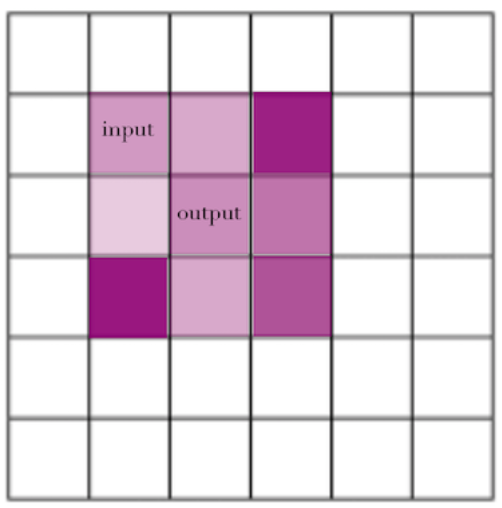
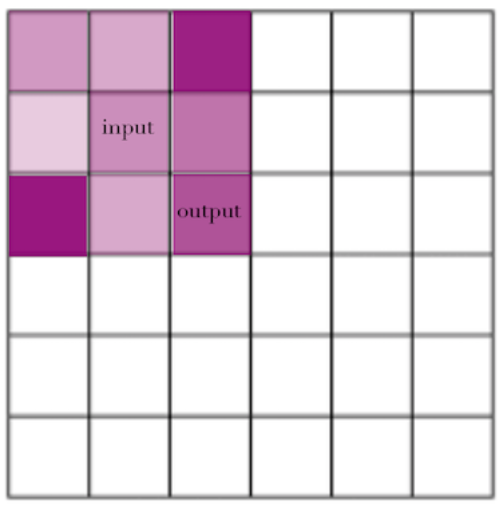
In cases where the kernel is symmetric, this doesn’t matter, but in typical convolution filters, symmetry isn’t the case: the weight for “to the right of the center, down by one” is different than the weight for “to the left of the center, up by one”, so if you simply took the the output-centered filter and tried to use it in a proper convolution framework, centered at the input point, you would get different weights.
You can see this more clearly in the visualization above, where we use an output-centered version of a g(x) kernel to generate weights for each input, and then an input-centered version, and see that you can’t use the same kernel as you’d use in one procedure in the other and get the same results.
This fact — that you can’t directly plug in output-centered kernels as the g(x) in a convolution equation — was the biggest persistent confusion for me around convolutions, because it seems like it’s doing so nearly the same thing, and because so many explanations use symmetric kernels, so the distinction isn’t highlighted.